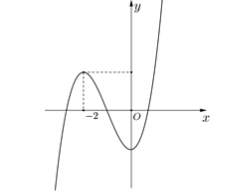
Cho hàm số $\large f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ

Cho hàm số $\large f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ bên dưới

Số điểm cực trị của hàm số $\large y = f(-2x^2 + 4x) $  là: 

• A. 5
• B. 2
• C. 4
• D. 3

Chọn A
Ta có: $\large y ' = (-2x^2 + 4x)'.f'(-2x^2 + 4x) = (-4x+4).f'(-2x^2+ 4x)$ 

Mặt khác: 

$\large -4x+ 4= 0\Leftrightarrow x = 1$  

$\large -2x^2 + 4x =0 \Leftrightarrow $  $\large \left[\begin{align}& x=0\\& x = 2\\\end{align}\right. $ 

$\large -2x^2 + 4x= -2\Leftrightarrow 2x^2 - 4x-2=0\Leftrightarrow $  $\large \left[\begin{align}& x =1-\sqrt{2}\\& x = 1+\sqrt{2}\\\end{align}\right. $ 

Đặt $\large t = -2x^2 + 4x\Rightarrow t' = -4x+ 4$ . Ta có bảng biến thiên của $\large t = -2x^2 + 4x$ 

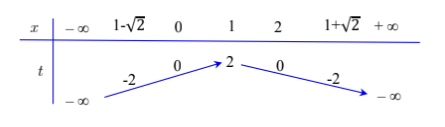
Dựa vào đồ thị của hàm số $\large f(x) = ax^3 + bx^2 + cx+ d$  ta suy ra bảng xét dấu của $\large y' = (-4x+ 4).f'( -2x^2 + 4x)$ 

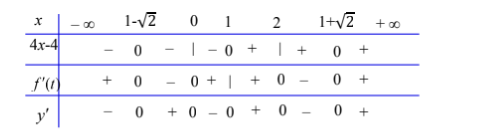
Từ bảng xét dấu trên ta suy ra: Hàm số đã cho có 5 cực trị