Cho hàm số f(x) có đạo hàm $\large f'(x) = x^2(x+1) ^3 (x-2)$. Số điểm

Cho hàm số f(x) có đạo hàm $\large f'(x) = x^2(x+1) ^3 (x-2)$. Số điểm cực trị của hàm số f(x) là: 

• A. 2
• B. 0
• C. 3
• D. 1

Chọn A

Ta có: $\large f'(x) = 0\Leftrightarrow $  $\large \left[\begin{align}& x =0\\& x= -1\\& x= 2\\\end{align}\right. $ (trong đó $\large x =0$  là nghiệm bội 2; $\large x =-1$  là nghiệm bội 3; $\large x = 2$  là nghiệm bội 1)

Bảng xét dấu f'(x)

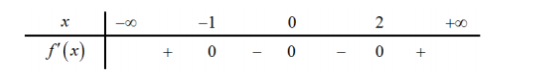
Từ bảng xét dấu, suy ra hàm số có 2 điểm cực trị